1.
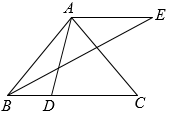
如图 , 在
, 在 中,
中, ,
,  沿
沿 方向向左平移得到
方向向左平移得到 ,
,  、
、 对应点分别是
对应点分别是 、
、 点
点 是线段
是线段 上的一个动点,连接
上的一个动点,连接 , 将线段
, 将线段 绕点
绕点 逆时针旋转至线段
逆时针旋转至线段 , 使得
, 使得 , 连接
, 连接 .
.
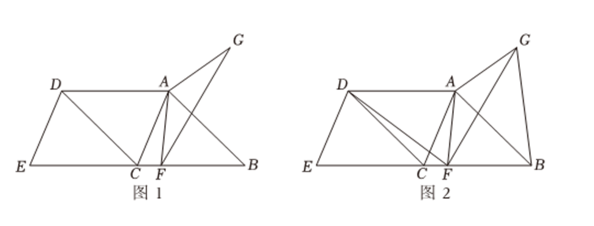
(1)
当点 与点
与点 重合时,求
重合时,求 的长;
(2)
如图
的长;
(2)
如图 , 连接
, 连接 、
、 在点
在点 的运动过程中:
的运动过程中:
 和
和 是否总是相等?若是,请你证明;若不是,请说明理由;
是否总是相等?若是,请你证明;若不是,请说明理由;
 当
当 的长为多少时,
的长为多少时, 能构成等腰三角形?
能构成等腰三角形?
【考点】
平行线的性质;
等腰三角形的性质;
平行四边形的判定与性质;
锐角三角函数的定义;
旋转的性质;
三角形全等的判定-SAS;