1.
已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.
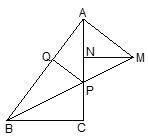
求证:
(1)
△APM是等腰三角形;
(2)
PC=AN.
【考点】
全等三角形的判定与性质;
角平分线的性质;
等腰三角形的判定与性质;
能力提升
真题演练