1.
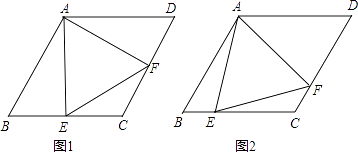
如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,将一个∠EDF=60°的三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转这个三角形纸片,使它的两边分别交CB,BA(或它们的延长线)于点E,F;
(1)
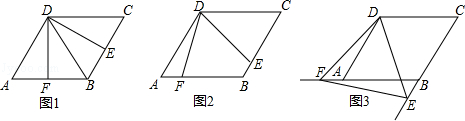
当CE=AF时,如图①,DE与DF的数量关系是;
(2)
继续旋转三角形纸片,当CE≠AF时,如图②,(1)的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(3)
再次旋转三角形纸片,当点E,F分别在CB,BA的延长线上时,如图③,请直接写出DE与DF的数量关系.
【考点】
全等三角形的判定与性质;
等边三角形的判定与性质;
菱形的性质;