1.
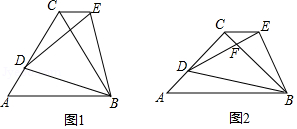
在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE=  ,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.
,点E在△ABC的内部,连接EC,EB和BD,并且∠ACE+∠ABE=90°.



(1)
如图1,当  =60°时,线段BD与CE的数量关系为,线段EA,EB,EC的数量关系为;
(2)
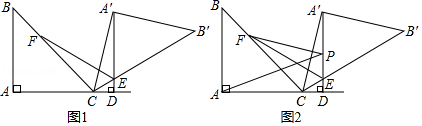
如图2当
=60°时,线段BD与CE的数量关系为,线段EA,EB,EC的数量关系为;
(2)
如图2当  =90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
(3)
在(2)的条件下,当点E在线段CD上时,若BC=
=90°时,请写出线段EA,EB,EC的数量关系,并说明理由;
(3)
在(2)的条件下,当点E在线段CD上时,若BC=  ,请直接写出△BDE的面积.
,请直接写出△BDE的面积.
【考点】
全等三角形的判定与性质;
等边三角形的判定与性质;
相似三角形的判定与性质;
等腰直角三角形;