1.
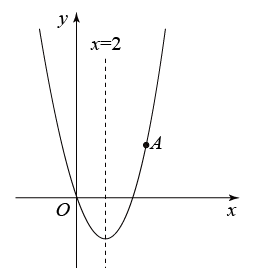
抛物线  经过点A(3
经过点A(3  ,0) 和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.
,0) 和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.

(1)
求抛物线的解析式;
(2)
连接AB、AC、BC,求△ABC的面积.
【考点】
待定系数法求一次函数解析式;
待定系数法求二次函数解析式;
二次函数与一次函数的综合应用;
能力提升
真题演练