如图矩形ABCO，点A，C分别在y轴与x轴的正半轴上，O为坐标原点，B的坐标为(6，4)，点D(0，1)，点P为边AB上一个动点，过点D，P的圆⊙M与AB相切，⊙M交x轴于点E，连接AM．

0 返回出卷网首页

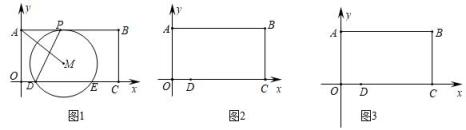
1. 如图矩形ABCO，点A，C分别在y轴与x轴的正半轴上，O为坐标原点，B的坐标为(6，4)，点D(0，1)，点P为边AB上一个动点，过点D，P的圆⊙M与AB相切，⊙M交x轴于点E，连接AM．

(1) 当P为AB的中点时，求DE的长及⊙M的半径；

(2) 当AM⊥DP时，求点P的坐标与⊙M的半径；

(3) 是否存在一点P使⊙M与矩形ABCO的另一条边也相切，若存在求出所有符合条件的点P的坐标．

【考点】

勾股定理; 切线的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．

(1) 求证：直线CD为⊙O的切线；

(2) 当AB=2BE，且CE= $\text{[math]}$ 时，求AD的长．

综合题普通

2. 如图所示，在Rt△ABC中，∠B=90°，AB=6cm，CB=3cm，点P在AC上以 $\text{[math]}$ cm/s的速度从点A匀速运动至点C停止，点Q沿BA方向以2cm/s的速度运动，当点P不与点A重合时，连结PQ，以PQ、BQ为邻边作平行四边形PQBM，当P点停止运动时，点Q也随之停止运动，设点P的运动时间为t(s)．

(2) 当四边形PQBM为矩形时，求t的值；

(3) 当△PQM是钝角三角形时，求t的取值范围．

综合题普通

3. 如图，在每个小正方形的边长均为1的方格纸中，有线段AB，点A、B均在小正方形的顶点上．

(1) 在方格纸中画出以AB为一边的直角△ABC，点C在小正方形的顶点上，且△ABC的面积为3．

(2) 在方格纸中将△ABC绕点C逆时针旋转90°，画出旋转后△DEC（点A与点D对应，点B与点E对应），请直接写出点A绕着点C旋转的路径长．

综合题普通