1.
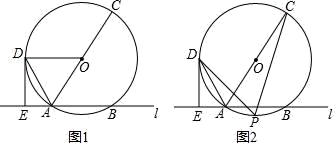
如图1，直线l与圆O相交于A ， B两点，AC是圆O的直径，D是圆上一点．DE⊥l于点E ， 连接AD ， 且AD平分∠CAE ．
(1)
求证：DE是圆O的切线．
(2)
若DE＝3，AE＝ 
，求圆O的半径．
(3)
如图2，在（2）的条件下，点P是弧AB上一点，连接PC ， PD ， PB ， 问：线段PC、PD、PB之间存在什么数量关系？请说明理由．
【考点】
全等三角形的判定与性质;
角平分线的性质;
圆内接四边形的性质;
切线的判定;
相似三角形的判定与性质;
