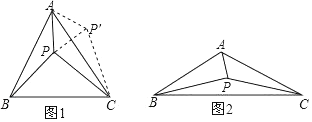
如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，2 ，，△ADP沿点A旋转至△ABP’，连接PP’，并延长AP与BC相交于点Q．

0 返回出卷网首页

1. 如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，2 $\text{[math]}$ ， $\text{[math]}$ ，△ADP沿点A旋转至△ABP’，连接PP’，并延长AP与BC相交于点Q．

(1) 求证：△APP’是等腰直角三角形；

(2) 求∠BPQ的大小；

(3) 求CQ的长．

【考点】

解直角三角形; 旋转的性质; 等腰直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 在△ABC中，AB=AC，∠BAC=α，点P是△ABC内一点，且∠PAC+∠PCA= $\text{[math]}$ ，连接PB，试探究PA、PB、PC满足的等量关系．

(1) 当α=60°时，将△ABP绕点A逆时针旋转60°得到△ACP′，连接PP′，如图1所示．由△ABP≌△ACP′可以证得△APP′是等边三角形，再由∠PAC+∠PCA=30°可得∠APC的大小为度，进而得到△CPP′是直角三角形，这样可以得到PA、PB、PC满足的等量关系为；

(2) 如图2，当α=120°时，参考（1）中的方法，探究PA、PB、PC满足的等量关系，并给出证明；

(3) PA、PB、PC满足的等量关系为．

综合题普通

2. 图①是一种手机平板支架、由托板、支撑板和底座构成，手机放置在托板上，图②是其侧面结构示意图、托板长 $\text{[math]}$ ，支撑板长 $\text{[math]}$ ，板 $\text{[math]}$ 固定在支撑板顶点C处，且 $\text{[math]}$ ，托板 $\text{[math]}$ 可绕点C转动，支撑板 $\text{[math]}$ 可绕点D转动， $\text{[math]}$ ．

(1) 若 $\text{[math]}$ 时，求点A到直线 $\text{[math]}$ 的距离（计算结果精确到个位）；

(2) 为了观看舒适，把（1）中 $\text{[math]}$ 调整为 $\text{[math]}$ ，再将 $\text{[math]}$ 绕点D逆时针旋转，使点B落在直线 $\text{[math]}$ 上即可、求 $\text{[math]}$ 旋转的角度．

（参考数： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

综合题普通

3. 在平面直角坐标系中，点A的坐标为（1，0），点B的坐标为（0， $\text{[math]}$ ），把△ABO绕原点O顺时针旋转，得到△A'B'O，记旋转角为α.

(1) 如图1，当α=30°时，求点B'的坐标.

(2) 设直线AA'与直线BB′相交于点M，如图2，当α=90°时，求点M的坐标.

综合题困难