1.
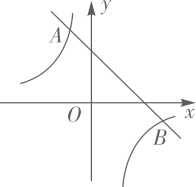
如图,一次函数  的图象与反比例函数
的图象与反比例函数  的图象相交于
的图象相交于  、
、  两点,其中点
两点,其中点  的坐标为
的坐标为  ,点
,点  的坐标为
的坐标为  .
.
(1)
根据图象,直接写出满足  的
的  的取值范围;
(2)
求这两个函数的表达式;
(3)
点
的取值范围;
(2)
求这两个函数的表达式;
(3)
点  在线段
在线段  上,且
上,且  ,求点
,求点  的坐标.
的坐标.
【考点】
待定系数法求一次函数解析式;
一次函数与不等式(组)的关系;
待定系数法求反比例函数解析式;
能力提升