如图，四边形ABCD中，AC⊥BD交BD于点E，点F，M分别是AB，BC的中点，BN平分∠ABE交AM于点N，AB＝AC＝BD.连接MF，NF.

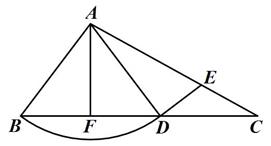
1. 如图，四边形ABCD中，AC⊥BD交BD于点E，点F，M分别是AB，BC的中点，BN平分∠ABE交AM于点N，AB＝AC＝BD.连接MF，NF.

(1) 判断△BMN的形状，并证明你的结论；

(2) 判断△MFN与△BDC之间的关系，并说明理由.

【考点】

三角形内角和定理; 三角形的外角性质; 等腰三角形的性质; 相似三角形的判定; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

综合题普通

综合题普通

3. 在 $\text{[math]}$ 中， $\text{[math]}$ ，在射线 $\text{[math]}$ 上取点D，E，且 $\text{[math]}$ ，作 $\text{[math]}$ ，使 $\text{[math]}$ .

①若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

②若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

综合题困难