0 返回出卷网首页
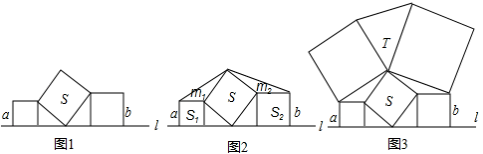
1. 在直线l上摆放着三个正方形

(1) 如图1，已知水平放置的两个正方形的边长依次是a，b斜着放置的正方形的面积S＝，两个直角三角形的面积和为；(均用a，b表示)
(2) 如图2，小正方形面积S1＝1，斜着放置的正方形的面积S＝4，求图中两个钝角三角形的面积m1和m2 ， 并给出图中四个三角形的面积关系；
(3) 图3是由五个正方形所搭成的平面图，T与S分别表示所在的三角形与正方形的面积，试写出T与S的关系式，并利用(1)和(2)的结论说明理由.
【考点】
三角形的面积; 全等三角形的判定与性质; 勾股定理的应用; 正方形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 某数学兴趣小组开展了一次课外活动，过程如下：如图1，正方形ABCD中，AB=6，将三角板放在正方形ABCD上，使三角板的直角顶点与D点重合.三角板的一边交AB于点P，另一边交BC的延长线于点Q.

(1) 求证：DP=DQ；
(2) 如图2，小明在图1的基础上作∠PDQ的平分线DE交BC于点E，连接PE，他发现PE和QE存在一定的数量关系，请猜测他的结论并予以证明；
(3) 如图3，固定三角板直角顶点在D点不动，转动三角板，使三角板的一边交AB的延长线于点P，另一边交BC的延长线于点Q，仍作∠PDQ的平分线DE交BC延长线于点E，连接PE，若AB：AP=3：4，请帮小明算出△DEP的面积.
综合题 普通
2. 如图1，在正方形ABCD中，AD=6，点P是对角线BD上任意一点，连接PA，PC过点P作PE⊥PC交直线AB于E．

(1) 求证：PC=PE；
(2) 延长AP交直线CD于点F.

①如图2，若点F是CD的中点，求△APE的面积；

②若ΔAPE的面积是 ，则DF的长为
(3) 如图3，点E在边AB上，连接EC交BD于点M，作点E关于BD的对称点Q，连接PQ，MQ，过点P作PN∥CD交EC于点N，连接QN，若PQ=5，MN= ，则△MNQ的面积是
综合题 困难
3. 如图，正方形ABCD的对角线AC，BD相交于点O，延长CB至点F，使CF=CA，连接AF，∠ACF的平分线分别交AF，AB，BD于点E，N，M，连接EO．


(1) 已知BD= ，求正方形ABCD的边长；
(2) 猜想线段EM与CN的数量关系并加以证明．
综合题 普通