1.
如图,在四边形  中
中  ,
,  ,
,  ,点
,点  为边
为边  上一点,将
上一点,将  沿
沿  翻折,点
翻折,点  落在对角线
落在对角线  上的点
上的点  处,连接
处,连接  并延长交射线
并延长交射线  于点
于点  .
.
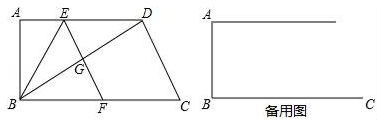
(1)
如果  ,求
,求  的长;
(2)
当点
的长;
(2)
当点  在边
在边  上时,连接
上时,连接  ,设
,设  ,求
,求  关于
关于  的函数关系式并写出
的函数关系式并写出  的取值范围;
(3)
连接
的取值范围;
(3)
连接  ,如果
,如果  是等腰三角形,求
是等腰三角形,求  的长.
的长.
【考点】
函数的概念;
函数解析式;
函数自变量的取值范围;
函数的表示方法;
三角形的面积;
等腰三角形的性质;
翻折变换(折叠问题);
解直角三角形;
能力提升