如图，在同一平面上，两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起，使斜边AC完全重合，且顶点B，D分别在AC的两旁，∠ABC=∠ADC=90°，∠CAD=30°，AB=BC=4cm（参考数据sin75°= ， sin15°=）

0 返回出卷网首页

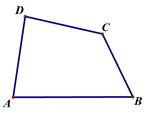
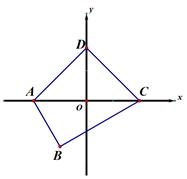
1. 如图，在同一平面上，两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起，使斜边AC完全重合，且顶点B，D分别在AC的两旁，∠ABC=∠ADC=90°，∠CAD=30°，AB=BC=4cm

（参考数据sin75°= ， sin15°=）

(1) AD= （cm），DC= （cm）

(2) 点M，N分别从A点，C点同时以每秒1cm的速度等速出发，且分别在AD，CB上沿A→D，C→B方向运动，点N到AD的距离（用含x的式子表示）

(3) 在（2）的条件下，取DC中点P，连接MP，NP，设△PMN的面积为y（cm2），在整个运动过程中，△PMN的面积y存在最大值，请求出y的最大值．

【考点】

二次函数的最值; 含30°角的直角三角形; 勾股定理; 锐角三角函数的定义; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知抛物线的解析式为y=﹣ $\text{[math]}$ x²+bx+5．

(1) 当自变量 x≥2时，函数值y 随 x的增大而减少，求b 的取值范围；

(2) 如图，若抛物线的图象经过点A（2，5），与x 轴交于点C，抛物线的对称轴与x 轴交于B．

①求抛物线的解析式；

②在抛物线上是否存在点P，使得∠PAB=∠ABC？若存在，求出点P 的坐标；若不存在，请说明理由．

综合题困难

2. 我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.

(1) 已知：如图，四边形ABCD是“等对角四边形”， $\text{[math]}$ ，则∠C=；

(2) 已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=4 ， AD=3.求对角线AC的长；

(3) 已知：如图，在平面直角坐标系xOy中，四边形ABCD是“等对角四边形”，其中 $\text{[math]}$ ，点D在y轴上，抛物线 $\text{[math]}$ 过点A、C，点P在抛物线上，当满足 $\text{[math]}$ 的P点至少有3个时，总有不等式 $\text{[math]}$ 成立，求n 的取值范围.

综合题困难

3. 如图，我国某海域上有 $\text{[math]}$ 、 $\text{[math]}$ 两个小岛， $\text{[math]}$ 在 $\text{[math]}$ 的正东方向．有一艘渔船在点 $\text{[math]}$ 处捕鱼，在 $\text{[math]}$ 岛测得渔船在东北方向上，在 $\text{[math]}$ 岛测得渔船在北偏西 $\text{[math]}$ 的方向上，且测得 $\text{[math]}$ 、 $\text{[math]}$ 两处的距离为 $\text{[math]}$ 海里．

(1) 求 $\text{[math]}$ 、 $\text{[math]}$ 两处的距离；

(2) 突然，渔船发生故障，而滞留 $\text{[math]}$ 处等待救援．此时，在 $\text{[math]}$ 处巡逻的救援船立即以每小时 $\text{[math]}$ 海里的速度沿 $\text{[math]}$ 方向前往 $\text{[math]}$ 处，测得 $\text{[math]}$ 在小岛 $\text{[math]}$ 的北偏西 $\text{[math]}$ 方向上距 $\text{[math]}$ 岛 $\text{[math]}$ 海里处．求救援船到达 $\text{[math]}$ 处所用的时间（结果保留根号）．

综合题普通