0 返回出卷网首页
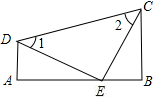
1. 如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC.

(1) 求证：△ABD≌△ECB；
(2) 若∠EDC=65°，求∠ECB的度数；
(3) 若AD=3，AB=4，求DC的长.
【考点】
平行线的性质; 全等三角形的判定与性质; 勾股定理;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，AD∥BC，∠A=90°，E是AB上的一点，且AD=BE，∠1=∠2．

(1) 求证：△ADE≌△BEC；
(2) 若AD=6，AB=14，请求出CD的长．
综合题 普通
2. 如图，四边形ABCD中，AB∥CD，过点D作DF⊥BC，垂足为F，DF与AC交于点M，已知∠1=∠2.

(1) 求证：CM=DM；
(2) 若FB=FC，求证：AM-MD=2FM.
综合题 普通
3. 已知：如图，C是AB上一点，点D，E分别在AB两侧，AD∥BE，且AD=BC，BE=AC．

(1) 求证：CD=CE；
(2) 连接DE，交AB于点F，猜想△BEF的形状，并给予证明．
综合题 普通