1.
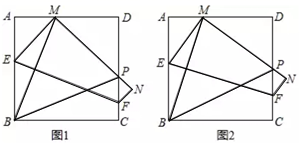
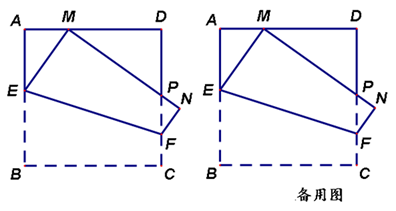
如图,在边长为1的正方形ABCD中,动点E,F分别在边AB,CD上,将正方形ABCD沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A,D重合),点C落在点N处,MN与CD交于点P,设BE=x.
(1)
当AM=  时,求x的值;
(2)
随着点M在边AD上位置的变化,ΔPDM的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;
(3)
若AM=a,四边形BEFC的面积为S,求S与a之间的函数表达式.
时,求x的值;
(2)
随着点M在边AD上位置的变化,ΔPDM的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;
(3)
若AM=a,四边形BEFC的面积为S,求S与a之间的函数表达式.
【考点】
全等三角形的判定与性质;
勾股定理;
正方形的性质;
翻折变换(折叠问题);
能力提升
真题演练