1.
如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动,动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.
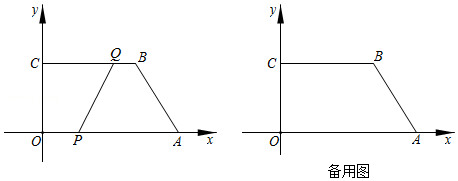
(1)
直接写出y关于t的函数解析式及t的取值范围:,
(2)
当PQ=3  时,求t的值,
(3)
连接OB交PQ于点D,若双曲线y=
时,求t的值,
(3)
连接OB交PQ于点D,若双曲线y=  (k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值,若变化,请说明理由.
(k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值,若变化,请说明理由.
【考点】
相似三角形的判定与性质;
解直角三角形;
反比例函数图象上点的坐标特征;
二次函数的实际应用-几何问题;
能力提升


