0 返回出卷网首页
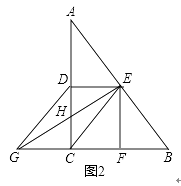
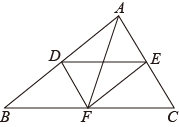
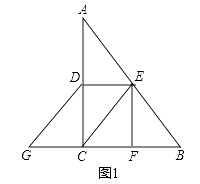
1. 如图，在▱ABCD中，∠ABD＝90°，延长AB至点E，使BE＝AB，连接CE．

(1) 求证：四边形BECD是矩形；
(2) 连接DE交BC于点F，连接AF，若CE＝2，∠DAB＝30°，求AF的长．
【考点】
平行四边形的判定与性质; 三角形的中位线定理;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，已知CD为△ABC中线，E为CD上一点，连接AE并延长至点F，使 ， 连接BF、CF， ．

(1) 求证：四边形DBFC是平行四边形．
(2) 设四边形ABFC的面积为S，在不添加任何辅助线的情况下，请写出图中四个面积等于的三角形．
综合题 普通
2. 在△ABC中，∠C=90°，D是AC的中点，E是AB的中点，作EF⊥BC于F，延长BC至G，使CG=BF，连接CE、DE、DG．
(1) 如图1，求证：四边形CEDG是平行四边形

；
(2) 如图2，连接EG交AC于点H，若EG⊥AB，请直接写出图2中所有长度等于 GH的线段．

综合题 普通
3. 如图，在△ABC中，点D、E、F分别是边AB、BC、CA的中点，AH是边BC上的高．

(1) 求证：四边形ADEF是平行四边形；
(2) 若∠AHF＝20°，∠AHD＝50°，求∠DEF的度数．
综合题 普通