如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°．点D是直线BC上的一个动点，连接AD，并以AD为边在AD的右侧作等边△ADE．

0 返回出卷网首页

1. 如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°．点D是直线BC上的一个动点，连接AD，并以AD为边在AD的右侧作等边△ADE．

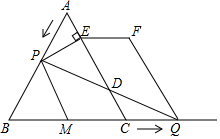
(1) 如图①，当点E恰好在线段BC上时，请判断线段DE和BE的数量关系，并结合图①证明你的结论；

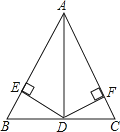
(2) 当点E不在直线BC上时，连接BE，其它条件不变，（1）中结论是否成立？若成立，请结合图②给予证明；若不成立，请直接写出新的结论；

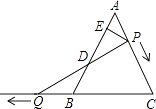
(3) 若AC=3，点D在直线BC上移动的过程中，是否存在以A、C、D、E为顶点的四边形是梯形？如果存在，直接写出线段CD的长度；如果不存在，请说明理由．

【考点】

全等三角形的判定与性质; 等边三角形的性质; 含30°角的直角三角形; 勾股定理; 梯形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在等边 $\text{[math]}$ 中， $\text{[math]}$ ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发以 $\text{[math]}$ 的速度沿 $\text{[math]}$ 匀速运动．动点 $\text{[math]}$ 同时从点 $\text{[math]}$ 出发以同样的速度沿 $\text{[math]}$ 的延长线方向匀速运动，当点 $\text{[math]}$ 到达点 $\text{[math]}$ 时，点 $\text{[math]}$ 同时停止运动．设运动时间为以 $\text{[math]}$ ．过点 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 边于 $\text{[math]}$ ．以 $\text{[math]}$ 为边作平行四边形 $\text{[math]}$ ．

(1) 当 $\text{[math]}$ 为何值时， $\text{[math]}$ 为直角三角形；

(2) 是否存在某一时刻 $\text{[math]}$ ，使点 $\text{[math]}$ 在 $\text{[math]}$ 的平分线上？若存在，求出 $\text{[math]}$ 的值，若不存在，请说明理由；

(3) 求 $\text{[math]}$ 的长；

(4) 取线段BC的中点M ，连接PM ，将△BMP 沿直线PM 翻折，得△B^' PM ，连接AB^' ，当t为何值时， AB^' 的值最小？并求出最小值．

综合题普通

如图，在△ABC中，AD平分∠BAC，且BD=CD，DE⊥AB于点E，DF⊥AC于点F．

(1) 求证：AB=AC；

(2) 若AD=2 $\text{[math]}$ ，∠DAC=30°，求AC的长．

综合题普通

3. 如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．

(1) 当∠BQD=30°时，求AP的长；

(2) 当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．

综合题普通