在Rt△ACB中，∠C=90°，点O是AB的中点，点M，N分别在边AC，BC上，OM⊥ON，连MN，AC=4，BC=8，设AM=a，BN=b，MN=c．

0 返回出卷网首页

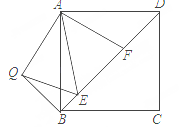
1. 在Rt△ACB中，∠C=90°，点O是AB的中点，点M，N分别在边AC，BC上，OM⊥ON，连MN，AC=4，BC=8，设AM=a，BN=b，MN=c．

(1) 求证：a²+b²=c²；

(2) ①若a=1，求b；②探究a与b的函数关系；

(3) △CMN面积的最大值为（不写解答过程）

【考点】

全等三角形的判定与性质; 勾股定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF=45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ，求证：

(1) EA是∠QED的平分线；

(2) EF²=BE²+DF² ．

综合题普通

2. 如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．

(1) 求证：AE=DC；

(2) 已知DC= $\text{[math]}$ ，求BE的长．

综合题普通

3. 如图，已知等腰直角△ABC，点P是斜边BC上一点(不与B，C重合)，PE是△ABP的外接圆⊙O的直径。

(1) 求证：△APE是等腰直角三角形；

(2) 若⊙O的直径为2，求PC²+PB²的值。

综合题普通