0 返回出卷网首页
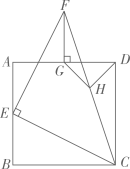
1. 已知：正方形ABCD的边长为4cm，点E从点A出发沿AD方向以1cm/秒的速度运动，与此同时，点F也从点D出发沿DC方向相同的速度运动，记运动的时间为t（0≤t≤4），AF与BE交于P点．

(1) 如图，在运动过程中，AF与BE相等吗？请说明理由．
(2) 在运动过程中，要使得△BPC是等腰三角形，t应为何值？请画出图形，并求出所有满足条件的t值．
【考点】
全等三角形的判定与性质; 等腰三角形的判定; 正方形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合）．以AD为边作正方形ADEF，连接CF．

(1) 如图1，当点D在线段BC上时，求证：①BD⊥CF．②CF=BC﹣CD．
(2) 如图2，当点D在线段BC的延长线上时，其它条件不变，请直接写出CF、BC、CD三条线段之间的关系；
(3) 如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系．②若连接正方形对角线AE、DF，交点为O，连接OC，探究△AOC的形状，并说明理由．
综合题 普通
2. 如图，正方形ABCD中，E是BD上一点，AE的延长线交CD于F，交BC的延长线于G，M是FG的中点.

(1) 求证：① ∠1=∠2；② EC⊥MC.
(2) 试问当∠1等于多少度时，△ECG为等腰三角形？请说明理由.
综合题 普通
3. 在△ABC中，AD平分∠BAC，E是BC上一点，BE=CD，EF∥AD交AB于F点，交CA的延长线于P，CH∥AB交AD的延长线于点H，

(1) 求证：△APF是等腰三角形；
(2) 猜想AB与PC的大小有什么关系？证明你的猜想。
综合题 普通