0 返回出卷网首页
1. 如图，AB是⊙O的直径，BC是⊙O的切线，切点为B，OC相交于点D，且CD=2，BC=4，

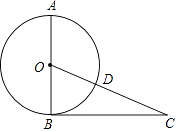
(1) 求⊙O的半径；
(2) 连接AD并延长，交BC于点E，取BE的中点F，连接DF，试判断DF与⊙O的位置关系，并说明理由．
【考点】
切线的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，PA，PB是⊙O的切线，A，B为切点，∠OAB=30度．

(1) 求∠APB的度数；
(2) 当OA=3时，求AP的长．
综合题 普通
2. 如图，已知MN是⊙O的直径，直线PQ与⊙O相切于P点，NP平分∠MNQ．

(1) 求证：NQ⊥PQ；
(2) 若⊙O的半径R=2，NP= ，求NQ的长．
综合题 普通
3. 如图，直线PM切⊙O于点M，直线PO交⊙O于A、B两点，弦AC∥PM，连接OM、BC．求证：

(1) △ABC∽△POM；
(2) 2OA2=OP•BC．
综合题 普通