如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°，AE=3 ，MN=2 ．

0 返回出卷网首页

1. 如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°，AE=3 $\text{[math]}$ ，MN=2 $\text{[math]}$ ．

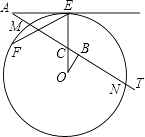
(1) 求∠COB的度数；

(2) 求⊙O的半径R；

(3) 点F在⊙O上（ $\text{[math]}$ 是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．

【考点】

含30°角的直角三角形; 勾股定理; 垂径定理; 切线的性质; 平移的性质; 相似三角形的判定与性质; 旋转的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图在 $\text{[math]}$ 中， $\text{[math]}$ ，在其内部有一点 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径的圆与 $\text{[math]}$ 相切于点 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ．

(2) 连接 $\text{[math]}$ ，若 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的半径．

综合题普通

2. 如图，AB为⊙O的直径，CB，CD分别切⊙O于点B，D，CD交BA的延长线于点E，CO的延长线交⊙O于点G，EF⊥OG于点F．

(1) 求证：∠FEB=∠ECF；

(2) 若BC=6，DE=4，求EF的长．

综合题普通

3. 如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D．

(1) 求证：DB=DE；

(2) 若AB=12，BD=5，求⊙O的半径．

综合题普通