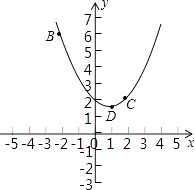1.
如图，抛物线 
与x轴交于点A和点B，与y轴交于点C，已知点B的坐标为（3，0）．
(1)
求a的值和抛物线的顶点坐标；
(2)
分别连接AC、BC．在x轴下方的抛物线上求一点M，使△AMC与△ABC的面积相等；
(3)
设N是抛物线对称轴上的一个动点，d=|AN﹣CN|．探究：是否存在一点N，使d的值最大？若存在，请直接写出点N的坐标和d的最大值；若不存在，请简单说明理由．
【考点】
待定系数法求二次函数解析式;
二次函数与一次函数的综合应用;
二次函数-动态几何问题;
二次函数y=a（x-h）²+k的性质;
二次函数y=ax²+bx+c与二次函数y=a（x-h）²+k的转化;
