1.
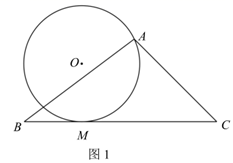
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.

(1)
求点P的坐标;
(2)
求抛物线解析式;
(3)
在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
【考点】
待定系数法求二次函数解析式;
等腰三角形的性质;
勾股定理;
切线的性质;
切线长定理;