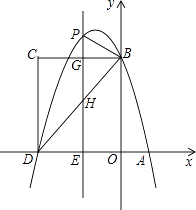
如图，在平面直角坐标系中，抛物线y=﹣ x2+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

0 返回出卷网首页

1. 如图，在平面直角坐标系中，抛物线y=﹣ $\text{[math]}$ x²+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

(1) 求该抛物线的解析式；

(2) 当点P在直线BC上方时，请用含m的代数式表示PG的长度；

(3) 在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

【考点】

待定系数法求一次函数解析式; 待定系数法求二次函数解析式; 相似三角形的性质; 二次函数与一次函数的综合应用; 二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知二次函数y=﹣x²+bx+c（c＞0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB=OC=3，顶点为M．

(1) 求二次函数的解析式；

(2) 点P为线段BM上的一个动点，过点P作x轴的垂线PQ，垂足为Q，若OQ=m，四边形ACPQ的面积为S，求S关于m的函数解析式，并写出m的取值范围；

(3) 探索：线段BM上是否存在点N，使△NMC为等腰三角形？如果存在，求出点N的坐标；如果不存在，请说明理由．

综合题困难

2. 如图，抛物线y=﹣x²+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y=﹣ $\text{[math]}$ x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．

(1) 求抛物线y=﹣x²+bx+c的表达式；

(2) 连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；

(3) 在（2）的前提下，y轴上是否存在一点H，使∠AHF=∠AEF？如果存在，求出此时点H的坐标，如果不存在，请说明理由．

综合题普通

3. 已知抛物线F：y＝x²+bx+c的图象经过坐标原点O，且与x轴另一交点为（ $\text{[math]}$ ，0）．

(1) 求抛物线F的解析式；

(2) 如图1，直线l：y $\text{[math]}$ x+m（m＞0）与抛物线F相交于点A（x₁ ， y₁）和点B（x₂ ， y₂）（点A在第二象限），求y₂﹣y₁的值（用含m的式子表示）；

(3) 在（2）中，若m $\text{[math]}$ ，设点A′是点A关于原点O的对称点，如图2．

①判断△AA′B的形状，并说明理由；

②平面内是否存在点P，使得以点A、B、A′、P为顶点的四边形是菱形？若存在，求出点P的坐标；若不存在，请说明理由．

综合题困难