1.
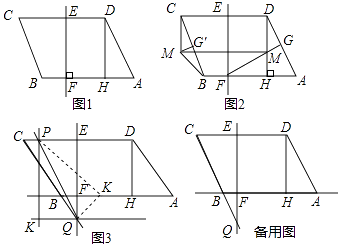
如图,在平面直角坐标系中,点A(a,0)是x轴正半轴上一点,PA⊥x轴,点B坐标为(0,b)(b>0),动点M在y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q,连结AQ,取AQ的中点为C.

(1)
若a=2b,点D坐标为(m,n),求  的值;
(2)
当点Q在线段BD上时,若四边形BQNC是菱形,面积为
的值;
(2)
当点Q在线段BD上时,若四边形BQNC是菱形,面积为  ,求经过点B,Q两点的直线解析式;
(3)
当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
,求经过点B,Q两点的直线解析式;
(3)
当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
【考点】
反比例函数的性质;
全等三角形的判定与性质;
平行四边形的性质;
菱形的性质;
相似三角形的判定与性质;
能力提升