如图：梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=6，在线段BC上任取一点P，连接DP，作射线PE⊥DP，PE与直线AB交于点E.

0 返回出卷网首页

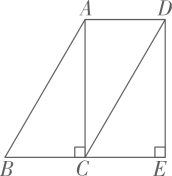
1. 如图：梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=6，在线段BC上任取一点P，连接DP，作射线PE⊥DP，PE与直线AB交于点E.

(1) 试确定当CP=3时，点E的位置；

(2) 若设CP=x，BE=y，试写出y关于自变量x的函数关系式.

【考点】

矩形的判定与性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在△ABC中，AD⊥BC于点D，点E为AC边的中点，过点A作AF∥BC，交DE的延长线于点F，连接CF．

(1) 如图1，求证：四边形ADCF是矩形；

(2) 如图2，当AB=AC时，取AB的中点G，连接DG、EG，在不添加任何辅助线和字母的条件下，请直接写出图中所有的平行四边形（不包括矩形ADCF）．

综合题普通

2. 定义：有一个内角为 $\text{[math]}$ ，且对角线相等的四边形称为准矩形．

(1) ① 如图1，准矩形 $\text{[math]}$ 中， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ；

②如图2，直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ，若整点 $\text{[math]}$ 使得四边形 $\text{[math]}$ 是准矩形，则点 $\text{[math]}$ 的坐标是；（整点指横坐标、纵坐标都为整数的点）

(2) 如图3，正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是边 $\text{[math]}$ 、 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是准矩形；

(3) 已知，准矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，当△ $\text{[math]}$ 为等腰三角形时，请直接写出这个准矩形的面积是．

综合题困难

3. 如图，在 $\text{[math]}$ ABCD中，∠ACB=90°，过点D作DE⊥BC交BC的延长线于点E．

(1) 求证：四边形ACED是矩形．

(2) 连接AE交CD于点F，连接BF．若∠ABC=60°，CE=2，则BF的长为

综合题普通