在平行四边形ABCD中，点E、F分别在AB、CD上，且AE=CF．

0 返回出卷网首页

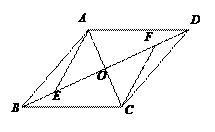
1. 在平行四边形ABCD中，点E、F分别在AB、CD上，且AE=CF．

(1)

求证：△ADE≌△CBF；

(2) 若DF=BF，试判定四边形DEBF是何种特殊四边形？并说明理由．

【考点】

平行线的性质; 三角形全等的判定; 菱形的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，A是∠MON边OM上一点，AE∥ON．

(1) 在图中作∠MON的角平分线OB，交AE于点B；（要求：尺规作图，保留作图痕迹，不写作法和证明）

(2) 在（1）中，过点A画OB的垂线，垂足为点D，交ON于点C，连接CB，将图形补充完整，并证明四边形OABC是菱形．

综合题普通

2. 如图，△BAD是由△BEC在平面内绕点B逆时针旋转60°而得，且AB⊥BC ， BE＝CE ，连接DE ．

(1) 求证：△BDE≌△BCE；

(2) 试判断四边形ABED的形状．并说明理由．

综合题普通

3. 如图，在▱ABCD中，AC、BD相交于点O，点E、F在BD上，且BE＝DF．连接AE、CF．

(1) 求证△AOE≌△COF；

(2) 若AC⊥EF，连接AF、CE，判断四边形AECF的形状，并说明理由．

综合题普通