已知抛物线y＝﹣2x2+bx+c与x轴交于A（2，﹣1），B（﹣1，﹣4）两点．

0 返回出卷网首页

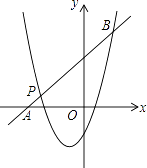
1. 已知抛物线y＝﹣2x²+bx+c与x轴交于A（2，﹣1），B（﹣1，﹣4）两点．

(1) 求抛物线的解析式；

(2) 用配方法求抛物线的顶点坐标．

【考点】

待定系数法求二次函数解析式; 二次函数y=ax²+bx+c与二次函数y=a（x-h）²+k的转化;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知：抛物线 $\text{[math]}$ 经过点P(−1，−2b)．

(1) 若b=−3，求这条抛物线的顶点坐标；

(2) 若b＜−3，过点P作直线PA⊥y轴，交y轴于点A，交抛物线于另一点B，且BP=3AP，求这条抛物线所对应的二次函数关系式．

综合题普通

2. 如图，在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ 和点B，与y轴交于点C．

(1) 求该抛物线的表达式和对称轴；

(2) 连接 $\text{[math]}$ ， D为x轴上方抛物线上一点（与点C不重合），如果 $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积相等，求点D的坐标；

(3) 设点 $\text{[math]}$ ，点E在抛物线的对称轴上（点E在顶点上方），当 $\text{[math]}$ ，且 $\text{[math]}$ 时，求点E的坐标．

综合题普通

3. 已知二次函数y₁=x²+mx+n的图象经过点P（﹣3，1），对称轴是经过（﹣1，0）且平行于y轴的直线．

(1) 求m，n的值．

(2) 如图，一次函数y₂=kx+b的图象经过点P，与x轴相交于点A，与二次函数的图象相交于另一点B，点B在点P的右侧，PA：PB=1：5，求一次函数的表达式．

(3) 直接写出y₁＞y₂时x的取值范围．

综合题普通