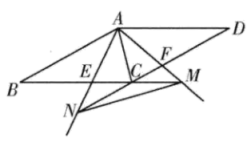
如图1，在△ABC中，AB＝AC＝20，tanB＝，点D为BC边上的动点（D不与点B，C重合）.以D为顶点作∠ADE＝∠B，射线DE交AC边于点E，过点A作AF⊥AD交射线DE于点F，连接CF.

0 返回出卷网首页

1. 如图1，在△ABC中，AB＝AC＝20，tanB＝ $\text{[math]}$ ，点D为BC边上的动点（D不与点B，C重合）.以D为顶点作∠ADE＝∠B，射线DE交AC边于点E，过点A作AF⊥AD交射线DE于点F，连接CF.

(1) 求证：△ABD∽△DCE；

(2) 当DE∥AB时（如图2），求AE的长；

(3) 点D在BC边上运动的过程中，是否存在某个位置，使得DF＝CF？若存在，求出此时BD的长；若不存在，请说明理由.

【考点】

等腰三角形的性质; 相似三角形的判定与性质; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是边 $\text{[math]}$ 的延长线上一点， $\text{[math]}$ 是边 $\text{[math]}$ 上一点，且 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 作 $\text{[math]}$ 于 $\text{[math]}$ 点，并连结DE.若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积.

综合题普通

2. 如图，已知等腰 $\text{[math]}$ ，点D、E分别在 $\text{[math]}$ 上，且 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 如果 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

3. 如图，在菱形ABCD中， $\text{[math]}$ 是锐角，点E是BC边上的动点（不与点B，C重合），将射线AE绕点A按逆时针方向旋转，交线段CD于点F．当 $\text{[math]}$ 时，延长线段BC交射线AF于点M，延长线段DC交射线AE于点N，连接AC．

(1) 求证： $\text{[math]}$ ；

(2) 连接MN，若 $\text{[math]}$ ， $\text{[math]}$ ，则当 $\text{[math]}$ 是以MN为腰的等腰三角形时，求CE的长．

综合题普通