0 返回出卷网首页
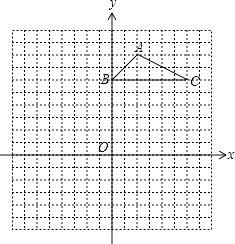
1. 在平面直角坐标系中，若点P（x，y）的坐标x、y均为整数，则称点P为格点，若一个多边形的顶点全是格点，则称该多边形为格点多边形．格点多边形的面积记为S，其内部的格点数记为N，边界上的格点数记为L，例如图中△ABC是格点三角形，对应的S=1，N=0，L=4．

(1) 求出图中格点四边形DEFG对应的S，N，L的值．
(2) 已知格点多边形的面积可表示为S=N+aL+b，其中a，b为常数，若某格点多边形对应的N=82，L=38，求S的值．
【考点】
点的坐标; 坐标与图形性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. 每个小方格都是边长为1的正方形，在平面直角坐标系中．

(1) 写出图中从原点O出发，按箭头所指方向先后经过的A、B、C、D、E这几个点点的坐标；
(2) 按图中所示规律，找到下一个点F的位置并写出它的坐标．
综合题 普通
2. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点都在格点上，建立平面直角坐标系．

(1) 点A的坐标为，点C的坐标为．
(2) 将△ABC向左平移7个单位，请画出平移后的△A1B1C1 ． 若M为△ABC内的一点，其坐标为（a，b），则平移后点M的对应点M1的坐标为．
(3) 以原点O为位似中心，将△ABC缩小，使变换后得到的△A2B2C2与△ABC对应边的比为1：2．请在网格内画出△A2B2C2 ， 并写出点A2的坐标：．
综合题 普通
3. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．根据所给定义解决下列问题：
(1) 若已知点D（1，2）、E（﹣2，1）、F（0，6），则这3点的“矩面积”=．
(2) 若D（1，2）、E（﹣2，1）、F（0，t）三点的“矩面积”为18，求点F的坐标．
综合题 普通