0 返回出卷网首页
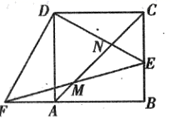
1. 边长为4的正方形ABCD中，点E是BC边上的一个动点，连接DE，交AC于点N，过点D作DF⊥DE，交BA的延长线于点F，连接EF，交AC于点M．

(1) 判定△DFE的形状，并说明理由；
(2) 设CE=x，△AMF的面积为y，求y与x之间的函数关系式；并求出当x为何值时y有最大值？最大值是多少？
(3) 随着点E在BC边上运动，NA·MC的值是否会发生变化？若不变，请求出NA·MC的值；若变化，请说明理由．
【考点】
全等三角形的判定与性质; 正方形的性质; 两条直线被一组平行线所截，所得的对应线段成比例; 相似三角形的判定与性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 正方形ABCD的边长为4，点E在BC上，点F在CD上，且CF＝BE，AE与BF交于G点.

(1) 如图1，求证：①AE＝BF，②AE⊥BF.
(2) 连接CG并延长交AB于点H，

①若点E为BC的中点（如图2），求BH的长；

②若点E在BC的边上滑动（不与B、C重合），当CG取得最小值时，求BE的长.
综合题 困难
2. 如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点(与点O不重合)，作AF⊥BE，垂足为G，交BC于F，交B0于H，连接OG，CC．


(1) 求证：AH=BE；
(2) 试探究：∠AGO的度数是否为定值?请说明理由；
(3) 若OG⊥CG，BG= ，求△OGC的面积．
综合题 普通
3. 如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交BC于G．

(1) 求证：BG=DE；
(2) 若点G为CD的中点，求 的值．
综合题 困难