已知四边形ABCD为矩形，对角线AC、BD相交于点O，AD＝AO．点E、F为矩形边上的两个动点，且∠EOF＝60°．

0 返回出卷网首页

1. 已知四边形ABCD为矩形，对角线AC、BD相交于点O，AD＝AO．点E、F为矩形边上的两个动点，且∠EOF＝60°．

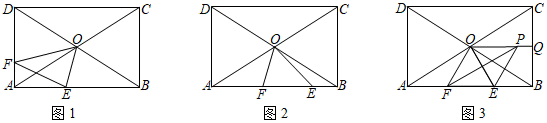
(1) 如图1，当点E、F分别位于AB、AD边上时，若∠OEB＝75°，求证：DF＝AE；

(2) 如图2，当点E、F同时位于AB边上时，若∠OFB＝75°，试说明AF与BE的数量关系；

(3) 如图3，当点E、F同时在AB边上运动时，将△OEF沿OE所在直线翻折至△OEP，取线段CB的中点Q．连接PQ，若AD＝2a（a＞0），则当PQ最短时，求PF之长．

【考点】

垂线段最短及其应用; 全等三角形的判定与性质; 矩形的性质; 解直角三角形; 旋转的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 将矩形ABCD绕点A顺时针旋转得到矩形AEFG，点E在BD上；

(1) 求证：FD＝AB；

(2) 连接AF，求证：∠DAF＝∠EFA.

综合题普通

2. 如图1，有一组平行线 $\text{[math]}$ ，正方形 $\text{[math]}$ 的四个顶点分别在 $\text{[math]}$ 上， $\text{[math]}$ 过点D且垂直于

于点E，分别交 $\text{[math]}$ 于点F，G， $\text{[math]}$ ．

(1) AE=，正方形ABCD的边长＝；

(2) 如图2，将 $\text{[math]}$ 绕点A顺时针旋转得到 $\text{[math]}$ ，旋转角为 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，以 $\text{[math]}$ 为边在的 $\text{[math]}$ 左侧作菱形 $\text{[math]}$ ，使点 $\text{[math]}$ 分别在直线 $\text{[math]}$ 上．

①写出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系并给出证明；

②若 $\text{[math]}$ =30°，求菱形 $\text{[math]}$ 的边长．

综合题困难

3. 如图，将矩形ABCD绕点A顺时针旋转θ（0°≤θ≤360°），得到矩形AEFG.

(1) 当点E在BD上时，求证：AF∥BD；

(2) 当GC＝GB时，求θ；

(3) 当AB＝10，BG＝BC＝13时，求点G到直线CD的距离.

综合题困难