1.
如图1,在  中,
中,  ,点D,E分别在边
,点D,E分别在边  上,且
上,且  ,连接
,连接  .现将
.现将  绕点A顺时针方向旋转,旋转角为
绕点A顺时针方向旋转,旋转角为  ,如图2,连接
,如图2,连接  .
.

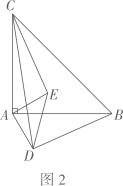
(1)
当  时,求证:
时,求证:  ;
(2)
如图3,当
;
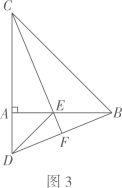
(2)
如图3,当  时,延长
时,延长  交
交  于点
于点  ,求证:
,求证:  垂直平分
垂直平分  ;
(3)
在旋转过程中,求
;
(3)
在旋转过程中,求  的面积的最大值,并写出此时旋转角
的面积的最大值,并写出此时旋转角  的度数.
的度数.
【考点】
三角形的面积;
全等三角形的判定与性质;
等腰三角形的性质;
线段垂直平分线的判定;
能力提升


