1.
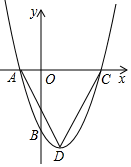
如图,抛物线  (
(  )过点
)过点  和
和  ,点B是抛物线的顶点,点D是x轴下方抛物线上的一点,连接
,点B是抛物线的顶点,点D是x轴下方抛物线上的一点,连接  ,
,  .
.
(1)
求抛物线的解析式;
(2)
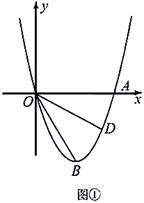
如图①,当  时,求点D的坐标;
(3)
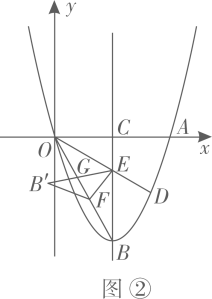
如图②,在(2)的条件下,抛物线的对称轴交x轴于点C,交线段
时,求点D的坐标;
(3)
如图②,在(2)的条件下,抛物线的对称轴交x轴于点C,交线段  于点E,点F是线段
于点E,点F是线段  上的动点(点F不与点O和点B重合,连接
上的动点(点F不与点O和点B重合,连接  ,将
,将  沿
沿  折叠,点B的对应点为点B,
折叠,点B的对应点为点B,  与
与  的重叠部分为
的重叠部分为  ,在坐标平面内是否存在一点
,在坐标平面内是否存在一点  ,使以点E,F,G,H为顶点的四边形是矩形?若存在,请直接写出点H的坐标,若不存在,请说明理由.
,使以点E,F,G,H为顶点的四边形是矩形?若存在,请直接写出点H的坐标,若不存在,请说明理由.
【考点】
待定系数法求二次函数解析式;
矩形的性质;
解直角三角形;
二次函数图象上点的坐标特征;
二次函数y=ax²+bx+c的性质;