如图，在矩形ABCD中，对角线相交于点O，⊙M为△BCD的内切圆，切点分别为N，P，Q，DN＝4，BN＝6．

0 返回出卷网首页

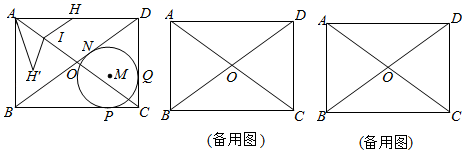
1. 如图，在矩形ABCD中，对角线相交于点O，⊙M为△BCD的内切圆，切点分别为N，P，Q，DN＝4，BN＝6．

(1) 求BC，CD；

(2) 点H从点A出发，沿线段AD向点D以每秒3个单位长度的速度运动，当点H运动到点D时停止，过点H作HI∥BD交AC于点I，设运动时间为t秒．

①将△AHI沿AC翻折得△A $\text{[math]}$ I，是否存在时刻t，使点 $\text{[math]}$ 恰好落在边BC上？若存在，求t的值；若不存在，请说明理由；

②若点F为线段CD上的动点，当△OFH为正三角形时，求t的值．

【考点】

勾股定理; 翻折变换（折叠问题）; 相似三角形的判定与性质; 四边形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，△ABC中，∠ACB=90°，tanA= $\text{[math]}$ ，点D是边AC上一点，连接BD，并将△BCD沿BD折叠，使点C恰好落在边AB上的点E处，过点D作DF⊥BD，交AB于点F．

(1) 求证：∠ADF=∠EDF；

(2) 探究线段AD，AF，AB之间的数量关系，并说明理由；

(3) 若EF=1，求BC的长．

综合题普通

2. 如图1，在矩形ABCD中，AD＝3，DC＝4，动点P在线段DC上以每秒1个单位的速度从点D向点C运动，过点P作PQ∥AC交AD于Q，将△PDQ沿PQ翻折得到△PQE.设点P的运动时间为t（s）．

(1) 当点E落在边AB上时，t的值为；

(2) 设△PQE与△ADC重叠部分的面积为s，求s与t的函数关系式；

(3) 如图2，以PE为直径作⊙O．当⊙O与AC边相切时，求CP的长．

综合题困难

3. 如图，在矩形ABCD中，AB＝3，AD＝1，点P在线段AB上运动，设AP＝ $\text{[math]}$ ，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．

(1) 当 $\text{[math]}$ ＝0时，折痕EF的长为；当点E与点A重合时，折痕EF的长为；

(2) 请写出使四边形EPFD为菱形的 $\text{[math]}$ 的取值范围，并求出当 $\text{[math]}$ ＝2时菱形的边长；

(3) 令EF²＝ $\text{[math]}$ ，当点E在AD、点F在BC上时，写出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式．当 $\text{[math]}$ 取最大值时，判断△EAP与△PBF是否相似？若相似，求出 $\text{[math]}$ 的值；若不相似，请说明理由．温馨提示：用草稿纸折折看，或许对你有所帮助哦！

综合题普通