0 返回出卷网首页
1. 如图，已知等边△ABC，请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：

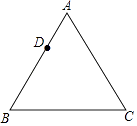
(1) 作△ABC的外心O；
(2) 设D是AB边上一点，在图中作出一个正六边形DEFGHI，使点F，点H分别在边BC和AC上．
【考点】
等边三角形的性质; 三角形的外接圆与外心; 正多边形的性质; 尺规作图-垂直平分线;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. 如图，△ABC是边长为2的正三角形，点D在△ABC内部，且满足DB=DC，DB⊥DC，点E在边AC上，延长ED交线段AB于点H．


(1) 若ED=EC请直接写出∠BAD=，∠AEH=，∠AHE=．
(2) 若ED=EC，求EH的长；
(3) 若AE=x，AH=y，请利用S△AEH=S△AED+S△AHD ， 求y关于x的函数关系式，并求自变量x的取值范围．
综合题 困难
2. 如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E，

(1) 求证：DE=DB；
(2) 若∠BAC=90°，BD=4，求△ABC外接圆的半径．
综合题 普通
3. 已知：在平面直角坐标系中，抛物线 交x轴于A、B两点，交y轴于点C，且对称轴为x=﹣2，点P（0，t）是y轴上的一个动点．

(1) 求抛物线的解析式及顶点D的坐标．
(2) 如图1，当0≤t≤4时，设△PAD的面积为S，求出S与t之间的函数关系式；S是否有最小值？如果有，求出S的最小值和此时t的值．
(3) 如图2，当点P运动到使∠PDA=90°时，Rt△ADP与Rt△AOC是否相似？若相似，求出点P的坐标；若不相似，说明理由．
综合题 困难