0 返回出卷网首页
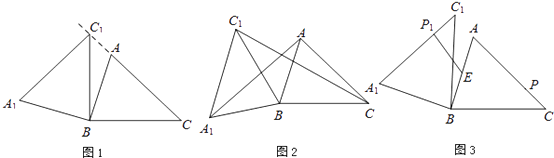
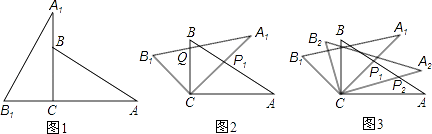
1. 将两块全等的三角板如图1摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．

(1) 将图1中△A1B1C绕点C顺时针旋转45°得图2，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；
(2) 在图2中，若AP1=a，则CQ等于多少？
(3) 将图2中△A1B1C绕点C顺时针旋转到△A2B2C（如图3），点P2是A2C与AP1的交点．当旋转角为多少度时，有△AP1C∽△CP1P2？这时线段CP1与P1P2之间存在一个怎样的数量关系？．
【考点】
全等三角形的判定与性质; 相似三角形的判定与性质; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图

(1) 问题发现

如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M.填空：

① 的值为；

②∠AMB的度数为.
(2) 类比探究

如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M.请判断 的值及∠AMB的度数，并说明理由；
(3) 拓展延伸

在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB= ，请直接写出当点C与点M重合时AC的长.
综合题 困难
2. 2012•义乌市）在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1 ．

(1) 如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；
(2) 如图2，连接AA1 ， CC1 ． 若△ABA1的面积为4，求△CBC1的面积；
(3) 如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1 ， 求线段EP1长度的最大值与最小值．
综合题 普通
3. 在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1 ， 旋转角为θ（0°＜θ＜90°），连接AC1、BD1 ， AC1与BD1交于点P．

(1) 如图1，若四边形ABCD是正方形．

①求证：△AOC1≌△BOD1 ．

②请直接写出AC1 与BD1的位置关系．
(2) 如图2，若四边形ABCD是菱形，AC=5，BD=7，设AC1=kBD1 ． 判断AC1与BD1的位置关系，说明理由，并求出k的值．
(3) 如图3，若四边形ABCD是平行四边形，AC=5，BD=10，连接DD1 ， 设AC1=kBD1 ． 请直接写出k的值和AC12+（kDD1）2的值．
综合题 困难