如图，△ABC中，AC=BC ， ∠ACB=90°，D为AC延长线上一点，连接BD ，在BC边上取一点E ，使得CD=CE ，连接AE并延长交BD于点F ．

0 返回出卷网首页

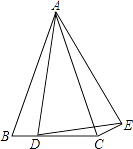
1. 如图，△ABC中，AC=BC ， ∠ACB=90°，D为AC延长线上一点，连接BD ，在BC边上取一点E ，使得CD=CE ，连接AE并延长交BD于点F ．

(1) 依题意补全图形；

(2) 求证：AF⊥BD；

(3) 连接CF ，点C 关于BD的对称点是Q ，连接FQ ，用等式表示线段CF ， CQ之间的数量关系，并加以证明．

【考点】

三角形全等及其性质; 三角形全等的判定; 等腰三角形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 如图 $\text{[math]}$ ，点 $\text{[math]}$ 、点 $\text{[math]}$ 分别是线段 $\text{[math]}$ 上两点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

(2) 如图 $\text{[math]}$ ，点 $\text{[math]}$ 、点 $\text{[math]}$ 分别是线段 $\text{[math]}$ 上两点，连接 $\text{[math]}$ 、 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 延长线于 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(3) 如图 $\text{[math]}$ ， $\text{[math]}$ 为射线 $\text{[math]}$ 上一点， $\text{[math]}$ 为射线 $\text{[math]}$ 上一点，且始终满足 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，猜想： $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系并证明你的结论．

综合题困难

2. 如图，已知E是平行四边形ABCD中BC边的中点，连接AE并延长AE交DC的延长线于点F．

(1) 求证：△ABE≌△FCE；

(2) 连接AC、BF，若AE= $\text{[math]}$ BC，求证：四边形ABFC为矩形；

(3) 在（2）条件下，直接写出当△ABC再满足时，四边形ABFC为正方形．

综合题普通

3. 如图，在△ABC中，AB=AC，点D为BC上一点，以AD为腰作等腰△ADE，AD=AE，∠BAC=∠DAE，连接CE．

(1) 求证：BD=CE；

(2) 已知BC=8，∠BAC=∠DAE=30°，若△DCE的面积为1，求线段BD的长．

综合题普通