0 返回出卷网首页
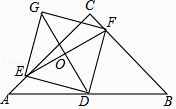
1. 如图，在等腰直角三角形ABC中，∠ACB=90°，AC=BC=4，D是AB的中点，E，F分别是AC，BC上的点（点E不与端点A，C重合），且AE=CF，连接EF并取EF的中点O，连接DO并延长至点G，使GO=OD，连接DE，DF，GE，GF．

(1) 求证：四边形EDFG是正方形；
(2) 当点E在什么位置时，四边形EDFG的面积最小？并求四边形EDFG面积的最小值．
【考点】
二次函数的最值; 全等三角形的判定与性质; 正方形的判定与性质; 等腰直角三角形;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 已知在四边形ABCD中，点E、F分别是BC、CD边上的一点．

(1) 如图1：当四边形ABCD是正方形时，且∠EAF＝45°，则EF、BE、DF满足的数量关系是，请说明理由；
(2) 如图2：当AB＝AD，∠B＝∠D＝90°，∠EAF是∠BAD的一半，问：（1）中的数量关系是否还存在？（填是或否）
(3) 在（2）的条件下，将点E平移到BC的延长线上，请在图3中补全图形，并写出EF、BE、DF的关系．
综合题 普通
2. 如图，在△ABC和△DBC中，∠ACB=∠DBC=90°，E是BC的中点，DE⊥AB，垂足为点F，且AB=DE．

(1) 求证：BD=BC；
(2) 若BD=6cm，求AC的长．
综合题 普通
3. 根据要求回答问题


(1) 发现：如图1，点A为线段BC外一动点，且BC=a，AB=b．

当点A位于时，线段AC的长取得最大值，且最大值为（用含a，b的式子表示）
(2) 应用：点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．

①请找出图中与BE相等的线段，并说明理由；

②直接写出线段BE长的最大值．
(3) 拓展：如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，请直接写出线段AM长的最大值及此时点P的坐标．
综合题 普通