如图，点A的坐标为（﹣8，0），点P的坐标为，直线y= x+b过点A，交y轴于点B，以点P为圆心，以PA为半径的圆交x轴于点C．

0 返回出卷网首页

1. 如图，点A的坐标为（﹣8，0），点P的坐标为 $\text{[math]}$ ，直线y= $\text{[math]}$ x+b过点A，交y轴于点B，以点P为圆心，以PA为半径的圆交x轴于点C．

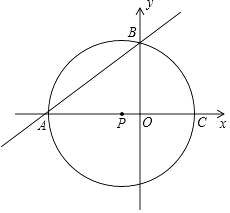
(1) 判断点B是否在⊙P上？说明理由．

(2) 求过A、B、C三点的抛物线的解析式；并求抛物线与⊙P另外一个交点为D的坐标．

(3) ⊙P上是否存在一点Q，使以A、P、B、Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．

【考点】

勾股定理; 圆的综合题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 是一条弦，D是 $\text{[math]}$ 的中点， $\text{[math]}$ 于点E，交 $\text{[math]}$ 于点F，交 $\text{[math]}$ 于点H， $\text{[math]}$ 交 $\text{[math]}$ 于点G．

(1) 求证： $\text{[math]}$ ．

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的半径．

综合题普通

2. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的切线．

(1) 尺规作图：过点B作 $\text{[math]}$ 的平行线交 $\text{[math]}$ 于点E，交 $\text{[math]}$ 于点F，连接 $\text{[math]}$ （保留作图痕迹，不写作法）；

(2) 证明： $\text{[math]}$ ；

(3) 若 $\text{[math]}$ 的半径长为 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的长．

综合题困难

3. 如图，四边形ABCD是⊙O的内接四边形，AB = 6，BC = 8，∠ABC = 90°，弧AD = 弧DC．

(1) 求边CD的长；

(2) 已知△ABE与△ABD关于直线AB对称．

①尺规作图：作△ABE；（保留作图痕迹，不写作法）

②连接DE，求线段DE的长．

综合题普通