0 返回出卷网首页
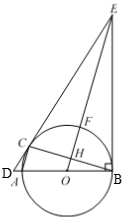
1. 如图，AB是⊙O的直径，C 是⊙O上一点，过点C 作⊙O的切线，交BA的延长线交于点D，过点B 作BE⊥BA，交DC延长线于点E，连接OE，交⊙O于点F，交BC于点H，连接AC.

(1) 求证：∠ECB=∠EBC；
(2) 连接BF，CF，若BF=5，sin∠FBC= ，求AC的长.
【考点】
线段垂直平分线的性质; 勾股定理; 锐角三角函数的定义; 切线长定理; 三角形的中位线定理;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. 如图，已知△ABC中，AB=BC=5，tan∠ABC= ．

(1) 求边AC的长；
(2) 设边BC的垂直平分线与边AB的交点为D，求 的值．
综合题 普通
2. 我们规定：三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“极化值”就等于AO2﹣BO2的值，可记为AB△AC=AO2﹣BO2 ．

(1) 在图1中，若∠BAC=90°，AB=8，AC=6，AO是BC边上的中线，则AB△AC=，OC△OA=；
(2) 如图2，在△ABC中，AB=AC=4，∠BAC=120°，求AB△AC、BA△BC的值；
(3) 如图3，在△ABC中，AB=AC，AO是BC边上的中线，点N在AO上，且ON= AO．已知AB△AC=14，BN△BA=10，求△ABC的面积．
综合题 普通
3. 如图，已知中， ， ， D是的中点，于点E，、的延长线交于点F．

(1) 求的正切值；
(2) 求的值．
综合题 普通