1.
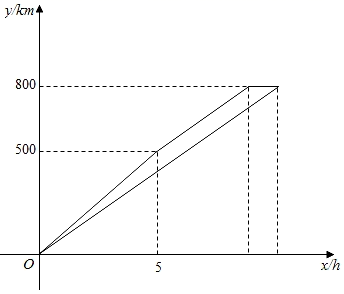
一辆货车从甲地到乙地,一辆轿车从乙地到甲地,两车沿同一条公路分别从甲、乙两地同时出发,匀速行驶.已知轿车比货车每小时多行驶20km.两车相遇后休息一段时间,再同时继续行驶.两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示的折线  ,结合图象回答下列问题:
,结合图象回答下列问题:

(1)
甲、乙两地之间的距离是km;
(2)
求两车的速度分别是多少km/h?
(3)
求线段  的函数关系式.直接写出货车出发多长时间,与轿车相距20km?
的函数关系式.直接写出货车出发多长时间,与轿车相距20km?
【考点】
待定系数法求一次函数解析式;
一次函数的实际应用;
通过函数图象获取信息;
能力提升
真题演练