如图，在△ABC中，点D、E分别在边BC、AC上，连接AD、DE，且∠B=∠ADE=∠C。

0 返回出卷网首页

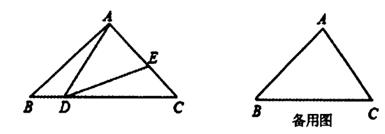
1. 如图，在△ABC中，点D、E分别在边BC、AC上，连接AD、DE，且∠B=∠ADE=∠C。

(1) 证明：△BDA∽△CED；

(2) 若∠B=45°，BC=6，当点D在BC上运动时(点D不与B、C重合)。且△ADE是等腰三角形，求此时BD的长。

【考点】

相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在△ABC和△ADE中，∠DAB＝∠EAC，∠C＝∠E.

(1) 求证：AD·BC＝AB·DE；

(2) 若 $\text{[math]}$ 求DE的长.

综合题普通

2. 如图，在 $\text{[math]}$ 中，直线DF与边AB相交于点D，与边AC相交于点E，与线段BC延长线相交于点F.

(1) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，其中m＞n＞0，求 $\text{[math]}$ 的值.

(3) 请根据上述（1）（2）的结论，猜想 $\text{[math]}$ =（直接写出答案，不需要证明）.

综合题困难

3. 如图所示，△ABC中，BD⊥AC于点D ， CE⊥AB于点E ， BD与CE相交于点F ．

(1) 求证：△BEF∽△CDF；

(2) 求证：DE·BF＝EF·BC ．

综合题普通