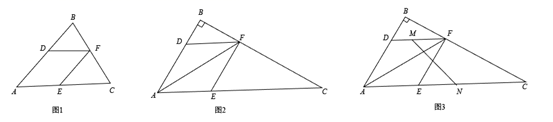
1.
如图,矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是.(a,b),且a,b满足于  +|b-8|=0,点D在CO上,连接BD,矩形OABC沿直线BD折叠,点C的对应点为点E,连接BE,DE,过点C作CF∥DE交BD于点F,连接EF。
+|b-8|=0,点D在CO上,连接BD,矩形OABC沿直线BD折叠,点C的对应点为点E,连接BE,DE,过点C作CF∥DE交BD于点F,连接EF。

(1)
如图1,求证:四边形CDEF为菱形;
(2)
如图2,当点C的对应点E正好落在对角线OB上时,求直线BD的解析式;
(3)
在(2)的条件下,将线段CF沿着CB的方向向右平移n个单位,且满足线段CF与矩形OABC的边有两个公共点时,直接写出点F的坐标和n的取值范围。
【考点】
待定系数法求一次函数解析式;
平行线的性质;
勾股定理;
平行四边形的判定与性质;
菱形的判定;
矩形的性质;
翻折变换(折叠问题);
一次函数的性质;