如图，直线AC∥BD，连结AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分.当动点P落在某个部分时，连结PA、PB，构成∠PAC、∠APB、∠PBD三个角.

0 返回出卷网首页

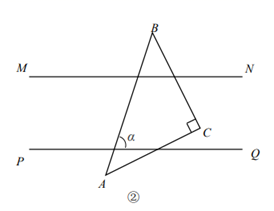
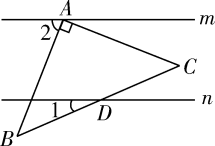
1. 如图，直线AC∥BD，连结AB，直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分.当动点P落在某个部分时，连结PA、PB，构成∠PAC、∠APB、∠PBD三个角.

(1) 当动点P落在第①部分时，有∠APB=∠PAC+∠PBD，请说明理由；

(2) 当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？请说明理由；

(3) 当动点P在第③部分时(点P不在直线AB上)，请探究∠APB、∠PAC、∠PBD 之间的关系.

【考点】

平行线的性质; 三角形的外角性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，已知 $\text{[math]}$ ，现将一直角三角形 $\text{[math]}$ 放入图中，其中 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$

(1) 当 $\text{[math]}$ 所放位置如图 $\text{[math]}$ 所示时，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为；

(2) 当 $\text{[math]}$ 所放位置如图 $\text{[math]}$ 所示时，求证： $\text{[math]}$ ；

(3) 在 $\text{[math]}$ 的条件下，若 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

综合题困难

2. 两条直线相交所形成的较小的角称为这两条直线的夹角.如：直线m、n相交，其夹角为60°，特别的，如果m⊥n，那么其夹角为90°.

(1) 如图①，MN∥PQ，含45°的直角三角形ABC的三边和两条平行线有4个交点D、E、F、G，若AB和PQ的夹角为65°，求∠CFQ与∠CEN的度数.

(2) 如图②，MN∥PQ，将一块含45°的直角三角板ABC任意摆放在两条平行线上（三角板足够大），使三角板的三边和两条平行线始终有4个交点.设斜边AB所在直线与MN（或PQ）的夹角为α（0°＜α≤90°），直接写出4个交点处的夹角之和.（结果可以用含α的代数式表示）

综合题困难

3. 问题情境：如图1， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

小明的思路是：过P作 $\text{[math]}$ ，通过平行线性质来求 $\text{[math]}$ .

(1) 按小明的思路，易求得 $\text{[math]}$ 的度数为度：（直接写出答案）

(2) 问题迁移：如图2， $\text{[math]}$ ，点P在射线 $\text{[math]}$ 上运动，记 $\text{[math]}$ ， $\text{[math]}$ ，当点P在B、D两点之间运动时，问 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 之间有何数量关系？请说明理由；

(3) 在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系.

综合题困难