1.
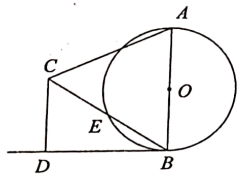
如图1,AB是⊙O的直径,点E是⊙O上一动点,且不与A,B两点重合,∠EAB的平分线交⊙O于点C,过点C作CD⊥AE,交AE的延长线于点D.

(1)
求证:CD是⊙O的切线;
(2)
求证:AC2=2AD•AO;
(3)
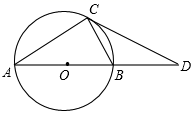
如图2,原有条件不变,连接BE,BC,延长AB至点M,∠EBM的平分线交AC的延长线于点P,∠CAB的平分线交∠CBM的平分线于点Q.求证:无论点E如何运动,总有∠P=∠Q.
【考点】
三角形的外角性质;
等腰三角形的性质;
圆周角定理;
切线的判定;
相似三角形的判定与性质;