如图，已知A、B、D在同一条直线上，且，

0 返回出卷网首页

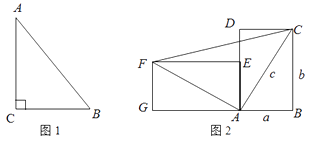
1. 如图，已知A、B、D在同一条直线上，且 $\text{[math]}$ ， $\text{[math]}$

(1) 求证： $\text{[math]}$ ；

(2) 若设 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，试利用这个图形验证勾股定理．

【考点】

勾股定理的证明; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 2000多年来，人们对直角三角形三边之间的关系的探究颇感兴趣，古往今来，下至平民百姓，上至帝王总统都愿意探究它，研究它的证明，新的证法不断出现下面给出几种探究方法（由若干个全等的直角三角形拼成以下图形）.

试用面积法选择其中一种推导直角三角形的三边a，b，c之间的数量关系.

(1) 三边a，b，c之间的数量关系为 .

综合题普通

2. 意大利著名画家达•芬奇用如图所示的方法证明了勾股定理，其中左图的空白部分是由两个正方形和两个直角三角形组成，右图的空白部分由两个直角三角形和一个正方形组成．设左图中空白部分的面积为S₁ ，右图中空白部分的面积为S₂ ．

(1) 请用含a ， b ， c的代数式分别表示S₁ ， S₂；

(2) 请利用达•芬奇的方法证明勾股定理．

综合题普通

3. 一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法.如图2，火柴盒的一个侧面ABCD倒下到AEFG的位置，连结CF，AB＝a，BC＝b，AC＝c.

(1) 请你结合图1用文字和符号语言分别叙述勾股定理；

(2) 请利用直角梯形BCFG的面积证明勾股定理： $\text{[math]}$ .

综合题普通