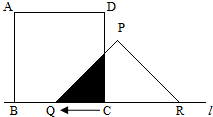
有一边长为6cm的正方形ABCD和等腰直角 PQR ， PQ＝PR ， QR＝8cm．点B ， C ， Q ， R在同一条直线上．当C ， Q两点重合时，等腰直角 PQR以1cm/秒的速度沿直线按箭头所示方向开始匀速运动，t秒后正方形ABCD与等腰直角 PQR重合部分的面积为Scm2 ．解答下列问题．

0 返回出卷网首页

1. 有一边长为6cm的正方形ABCD和等腰直角 $\text{[math]}$ PQR ， PQ＝PR ， QR＝8cm．点B ， C ， Q ， R在同一条直线 $\text{[math]}$ 上．当C ， Q两点重合时，等腰直角 $\text{[math]}$ PQR以1cm/秒的速度沿直线 $\text{[math]}$ 按箭头所示方向开始匀速运动，t秒后正方形ABCD与等腰直角 $\text{[math]}$ PQR重合部分的面积为Scm² ．解答下列问题．

(1) 当t＝3秒时，求S的值；当t＝6秒时，求S的值；

(2) 当6秒≤t≤8秒时，求s与t的函数关系式．

(3) 若重合部分的面积为15 $\text{[math]}$ 时，求t的值．

【考点】

正方形的性质; 相似三角形的判定与性质; 等腰直角三角形; 几何图形的面积计算-割补法; 四边形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 厘米， $\text{[math]}$ 厘米. 点 $\text{[math]}$ 沿 $\text{[math]}$ 边从 $\text{[math]}$ 开始向点 $\text{[math]}$ 以2厘米/秒的速度移动；点 $\text{[math]}$ 沿 $\text{[math]}$ 边从点 $\text{[math]}$ 开始向点 $\text{[math]}$ 以1厘米/秒速度移动.如果 $\text{[math]}$ 、 $\text{[math]}$ 同时出发，用 $\text{[math]}$ （秒）表示移动的时间 $\text{[math]}$ ，那么：

(1) 当 $\text{[math]}$ 为何值时， $\text{[math]}$ 为等腰直角三角形？

(2) 求四边形 $\text{[math]}$ 的面积；提出一个与计算结果有关的结论；

(3) 当 $\text{[math]}$ 为何值时，以点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 相似？

综合题困难

2. 如图，在四边形ABCD中，AC，BD相交于点E，点F在BD上，且 $\text{[math]}$ ， $\text{[math]}$ .

(1) 求证： $\text{[math]}$ .

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的面积为20，求 $\text{[math]}$ 的面积.

综合题普通

3. 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求 $\text{[math]}$ 的值；

(2) 如果 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积．

综合题普通