已知等边△ABC，D为BC边上一点，点E在线段AD上，且∠EBD＝∠BAD．将△ABE绕着点A逆时针旋转至△ACF，连接EF，交AC于点G．

0 返回出卷网首页

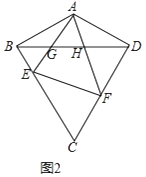
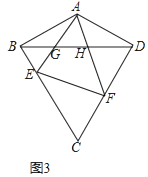
1. 已知等边△ABC，D为BC边上一点，点E在线段AD上，且∠EBD＝∠BAD．将△ABE绕着点A逆时针旋转至△ACF，连接EF，交AC于点G．

(1) 求∠AFE度数；

(2) 判断点E与直线BF位置关系并说明理由；

(3) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

【考点】

等边三角形的判定与性质; 相似三角形的判定与性质; 锐角三角函数的定义; 旋转的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在四边形ABCD中，AB=AD，BC=CD．

(1) 如图1，请连接AC，BD，求证：AC垂直平分BD；

(2) 如图2，若∠BCD=60°，∠ABC=90°，E，F分别为边BC，CD上的动点，且∠EAF=60°，AE，AF分别与BD交于G，H，求证：△AGH∽△AFE；

(3) 如图3，在（2）的条件下，若 EF⊥CD，直接写出 $\text{[math]}$ 的值．

综合题困难

2. 如图，在直角三角形ABC中，∠C＝90°，∠A＝30°，AC＝4，将△ABC绕点A逆时针旋转60°，使点B落在点E处，点C落在点D处．P、Q分别为线段AC、AD上的两个动点，且AQ＝2PC，连接PQ交线段AE于点M．

(1) AQ＝，△APQ为等边三角形；

(2) 是否存在点Q，使得△AQM、△APQ和△APM这三个三角形中一定有两个三角形相似？若存在请求出AQ的长；若不存在请说明理由；

(3) AQ＝，B、P、Q三点共线．

综合题普通

(1) 问题发现如图1，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ 交于点 $\text{[math]}$ .填空：① $\text{[math]}$ 的值为；② $\text{[math]}$ 的度数为.

(2) 类比探究如图2，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ .请判断 $\text{[math]}$ 的值及 $\text{[math]}$ 的度数，并说明理由；

(3) 拓展延伸在（2）的条件下，将 $\text{[math]}$ 绕点 $\text{[math]}$ 在平面内旋转， $\text{[math]}$ 所在直线交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出当点 $\text{[math]}$ 与点 $\text{[math]}$ 在同一条直线上时 $\text{[math]}$ 的长.

综合题困难